Breadth-First Search

Breadth-First Search (BFS) is a fundamental algorithm commonly used in graphs and trees. It forms the backbone of more advanced algorithms like Dijkstra's and A*. BFS is versatile, with applications such as detecting cycles in directed and undirected graphs, making it an essential tool in computer science.

Imagine you're researching your family tree. You have two parents, each of your parents has two parents, and so on. You could explore your ancestry in one of two ways:

• By path: Start with your mom, then your mom's mom, then your mom's mom's mom, and so on.
• By layers: Start with your parents, then move to your grandparents, then your great-grandparents, layer by layer.

The first method is an example of Depth-First Search (DFS), where you go as deep as possible along one path before backtracking. The second method is an example of Breadth-First Search (BFS), where you explore all the "neighbors" (parents) at the current layer before moving on to the next layer (grandparents). BFS focuses on layers rather than individual paths.

Applying BFS

How do we process a tree layer by layer programatically? This is where a Queue comes in handy. A queue is a FIFO (First-In, First-Out) data-structure that processes the oldest data first. Taking a look at this tree:

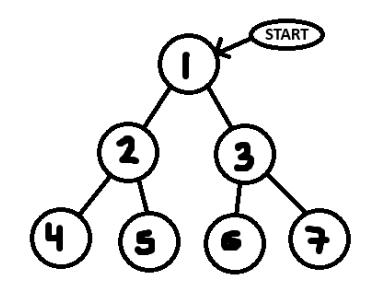
Starting off, we want to add the starting node (1) to a queue.

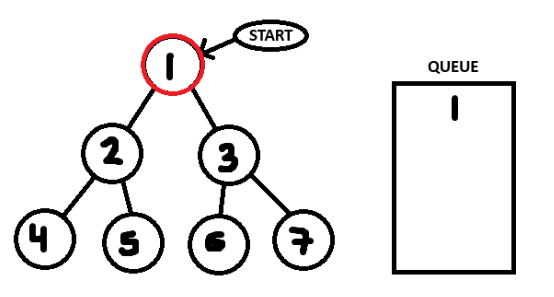
We can then pull the first item from the queue (1) and add it's neighbours into the queue (2, 3).

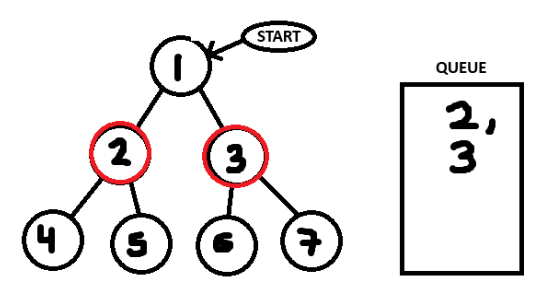
Then we can pull 2 from the queue and add it's neighbours (4, 5) to the queue.

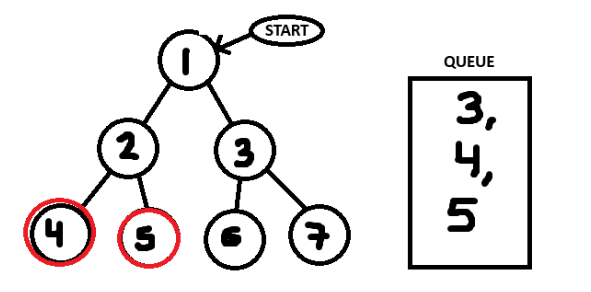
And finally we can pull 3 from the queue and add it's neighbours (6, 7) to the queue.

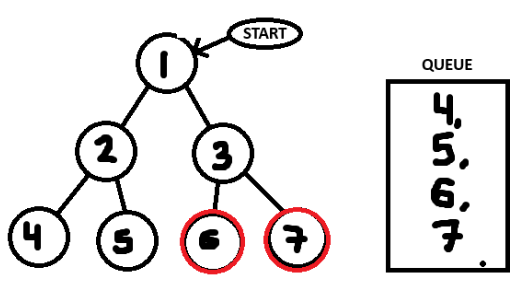
In summary, BFS explores each layer of a graph or tree systematically using a queue, ensuring all nodes at the current level are processed before moving deeper. This makes it an ideal algorithm for tasks requiring a shortest-path search or layered exploration.

The Code

Coding this out in a tree, we want to follow this pseudocode:

• Add the starting node to the queue
• While the queue is not empty
• Pop the first node from the queue
• Add the nodes neighbours to the queue

For this example, I'm also going to use a custom Node class that has left and right pointers.

    public class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int value) {
            this.value = value;
        }
    }
    
    public void BFS(Node start) {
        // Initialize the queue
        Queue queue = new LinkedList<>();

        // Add the start node to the queue
        queue.add(start);

        // Process the nodes in the queue until it's empty
        while (!queue.isEmpty()) {
            // Remove the first node from the queue and process it
            Node current = queue.poll();

            // Print the value
            System.out.print(current.value + " ");

            // Add the neighbours to the queue
            if (current.left!= null) {
                queue.add(current.left);
            }

            if (current.right!= null) {
                queue.add(current.right);
            }
        }
    }
        

    class Node:
        def __init__(self, value):
            self.value = value
            self.left = None
            self.right = None

    def BFS(node):
        # Initialize the queue
        queue = [node]
        # Process the nodes in the queue until it's empty
        while queue:
            # Remove the first node from the queue and process it
            current = queue.pop(0)

            # Print the value
            print(current.value)

            # Add the neighbours to the queue
            if current.left:
                queue.append(current.left)

            if current.right:
                queue.append(current.right)
        

    class Node {
        constructor(value) {
            this.value = value;
            this.left = null;
            this.right = null;
        }
    }

    const BFS = function(start) {
        // Initialize the queue
        const queue = [];
        // Add the start node to the queue
        queue.push(start);

        // Process the nodes in the queue until it's empty
        while (queue.length > 0) {
            // Remove the first node from the queue and process it
            const current = queue.shift();

            // Print the value
            console.log(current.value);

            // Add the neighbours to the queue
            if (current.left) {
                queue.push(current.left);
            }

            if (current.right) {
                queue.push(current.right);
            }
        }
    }
        

In this example, I used BFS on a tree. However in a graph a node may have multiple neighbours instead of just one neighbour. In this case, you would have to add an additional for loop inside of the while loop, that adds all of the nodes neighbours to the queue.