A* aka A-Star
A while back after diving into Dijkstra's algorithm, I decided to make Knights Travails. It's an application that when given a starting square and an end square on a chess board, find the shortest path for a knight--a piece that can only move in L's. You can check it out here if you'd like.
A* is very similar to Dijkstra's in that it's a "shortest path" algorithm, but the only difference is that it uses a heuristic to ensure that it's searching relatively in the right direction.
What's a heuristic?
Simply put, a heuristic is a rule or formula that helps guide the search process toward the goal more efficiently. For example, say you want to get from your house to a given McDonalds nearby. You could drive down every road in an attempt to find it which, let's be real you're probably hungry so that's not very practical. Another option is to use the addresses.
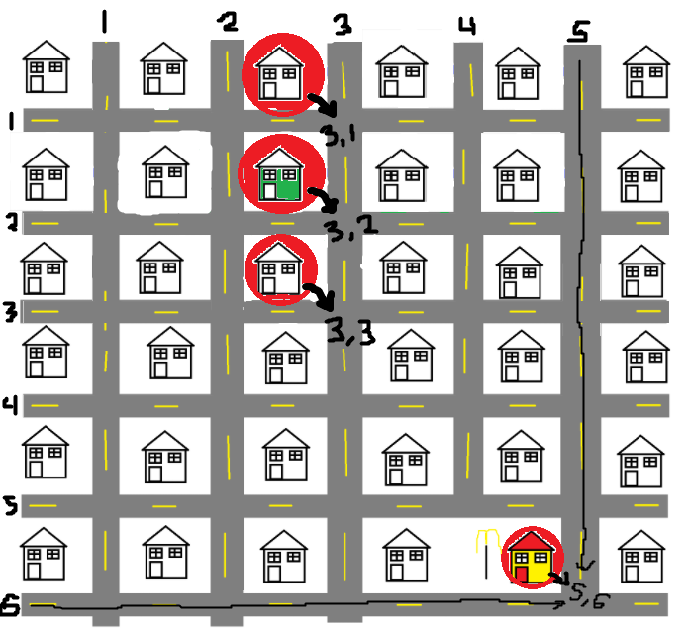
Say you're on 3rd Street and 2nd Ave and said McDonalds is on 5th Street and 6th Ave. By comparing the street numbers and ensuring that they're increasing towards your destination (ie 2nd -> 3rd -> 4th vs 2nd -> 1st), you're using a heuristic. Similarly, in A*, heuristics help algorithms focus on promising paths first, avoiding unnecessary exploration.

As you can see in my poorly drawn photo above, the issue with Dijkstra's is that it explores all possible paths whether or not the search is headed in the right direction. And it will continue to search until it's explored all potential routes. However we know that the bottom and right addresses are actually closer.

We could apply a heuristic (this particular one is known as the "Manhatten Distance") by using the (current x - destination x) + (current y - destination y). For example if say the first address we explored was the top house which is at 3rd and 1st, well then (3 - 5) + (1 - 6) = -7, whereas the bottom address that we explore would be located at 3rd and 3rd which would sum to (3 - 5) + (3 - 6) = -5.
One thing to note though, is that we use the absolute value meaning that the -5 and -7 become 5 and 7. The reason why is because non-negative numbers reflect the distance traveled irrespective of the direction traveled. So now we have a way to calculate which address is actually closer to McDonalds. There are other heuristics but today we'll give Manhattan Distance a go.
Applying the heuristic:
- Java
- Python
- JavaScript
public int heuristic(int[] current, int[] dest) {
// Compute how off the "x" direction is
int dx = Math.abs(current[0] - dest[0]);
// Compute how off the "y" direction is
int dy = Math.abs(current[1] - dest[1]);
// Add the two values together and return the result
return dx + dy;
}
def heuristic(current, dest):
# Compute how off the "x" direction is
dx = abs(current[0] - dest[0])
# Compute how off the "y" direction is
dy = abs(current[1] - dest[1])
# Add the two values together and return the result
return dx + dy
const heuristic = function(current, dest) {
const [currentSt, currentAve] = current;
const [destSt, destAve] = dest;
// Compute how off the "x" and "y" directions are
// Return the result
return Math.abs(currentSt - destSt) + Math.abs(currentAve - destAve);
}
Using the heuristic
Now that we have a heuristic, all we have to do is apply it. Going back to our example before with the addresses:
- Our house: 3rd St & 2nd Ave (3, 2)
- 1st Visited: 3rd St & 1st Ave (3, 1)
- 2nd Visited: 3rd St & 3rd Ave (3, 3)
- McDonalds: 6th St & 5th Ave (6, 5)
Traveling from our address to either the first visited or the second visited is exactly one step. If we add that value to the calculated heuristic, we get the total accumulated distance. In this case, the first would have an accumulated value of ((3 - 6) + (1 - 5)) + 1 and the second would have an accumulated value of ((3 - 6) + (3 - 5)) + 1 which would be 8 and 6 respectively.

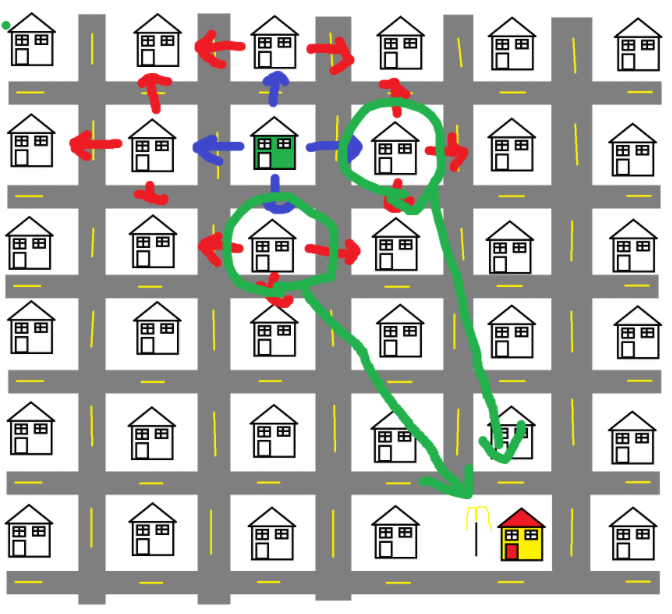
With the calculated values, we can put the addresses into a min-heap and use the calculated value in the comparator. This means that the first item in the heap will always be either the or one of the most promising routes to our destination. For reference, a heap is a type of tree that organizes its content based on a comparator. The comparator compares two pieces of data. For example, num1 < num2 or string1.length() > string2.length() are both comparators. Depending on how you compare the data determines whether the heap organizes the data from the smallest to the largest or vice-versa.
Putting all of this additional information together, we can now apply it to a Breadth-First Search. I've previously covered Breadth-First Search here but for a quick recap:
- Add the first node to a queue
- While the queue is not empty
- Pull the first item from the queue, check if it's our destination
- Add it's neighbours to the queue, rinse and repeat
- Java
- Python
- JavaScript
// start = [3, 2] = home, end = [6, 5] = McDonalds
public int[] BFS(int[] start, int[] dest) {
// Initialize the queue and a visited set
Queue queue = new LinkedList();
Set visited = new HashSet<>();
// An array for allowed directions
int[][] directions = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };
// Add the start address to the queue and mark it as visited
queue.offer(start);
// Note that since the set memory addresses, we need to use strings instead for the visited array
visited.add(Arrays.toString(start));
// Loop until the queue is empty or until we find the destination
while (!queue.isEmpty()) {
// Poll the first address in the queue
int[] current = queue.poll();
// Check if the current address is our destination
if (Arrays.equals(current, dest)) {
return current;
}
// Loop over all directions ie x + 1, x - 1, y + 1, y - 1
for (int[] dir : directions) {
int curX = current[0];
int curY = current[1];
// Add the direction to the current address
int nextX = curX + dir[0];
int nextY = curY + dir[1];
int[] neighbour = new int[] {nextX, nextY};
// Check if the neighbour has already been visited
if (visited.contains(Arrays.toString(neighbour))) {
continue;
}
// Mark as visited and add to the queue
visited.add(Arrays.toString(neighbour));
queue.offer(neighbour);
}
}
// Return an invalid address if the destination isn't reachable
return new int[] { -1, -1 };
}
# start = [3, 2] = home, end = [6, 5] = McDonalds
def BFS(start, dest):
# Initialize the queue and a visited set
queue = []
visited = set()
# An array for allowed directions
directions = [[1, 0], [-1, 0], [0, 1], [0, -1]]
# Add the start address to the queue and mark it as visited
queue.append(start)
visited.add(str(start))
while queue:
# Poll the first address in the queue
current = queue.pop(0)
# Check if the current address = to the destination address
if current == dest:
return current
# Loop over all directions ie x + 1, x - 1, y + 1, y - 1
for dir in directions:
curX = current[0]
curY = current[1]
nextX = curX + dir[0]
nextY = curY + dir[1]
# Check if the neighbour has already been visited
neighbour = [nextX, nextY];
if visited.contains(str(neighbour)):
continue
# Mark as visited and add to the queue
visited.add(str(neighbour))
queue.append(neighbour)
// start = [3, 2] = home, end = [6, 5] = McDonalds
const BFS = function(start, dest) {
// Initialize the queue and visited set
const queue = [];
const visited = new Set();
// An array for allowed directions
const directions = [[1, 0], [-1, 0], [0, 1], [0, -1]];
// Add the start address to the queue and mark it as visited
queue.push(start);
visited.add(JSON.stringify(start));
// Loop until the queue is empty or until we find the destination
while (queue.length > 0) {
const current = queue.shift();
// If the current address = to the destination address, return it
if (JSON.stringify(current) === JSON.stringify(dest)) {
return current;
}
// Loop over all directions ie x + 1, x - 1, y + 1, y - 1
for (const dir of directions) {
const curX = current[0];
const curY = current[1];
const nextX = curX + dir[0];
const nextY = curY + dir[1];
// Check if the neighbour has already been visited
const neighbour = [nextX, nextY];
if (visited.has(JSON.stringify(neighbour))) {
continue;
}
// Mark as visited and add to the queue
visited.add(JSON.stringify(neighbour));
queue.push(neighbour);
}
}
return [-1, -1];
}
Implementing A*
Above are the examples for BFS. As mentioned before though, there's only two minor differences between A* and BFS and that's applying our heuristic from before and using a min-heap over a queue for exploring neighbors. Additionally, we're going to use a custom node class to keep track of the address, accumulated cost, previously visisted address and the distance we've traveled so far. The nice thing with the previous variable is that we can use it to re-trace the path we took.
The general outline for A* is as follows:
- Initialize a min-heap with our comparator
- Initialize a visited set
- Add the starting position to the heap and visited set
- While the min-heap is not empty
- Pull the smallest item from the heap and check if it's equal to our destination
- If not, loop over all neighbouring addresses
- Add the neighbour to the heap and compare neighbours using the accumulated value (heuristic + distance traveled) as well as to the visited set
- To keep track of the path, we're going to use a custom node with a previous variable
- Java
- Python
- JavaScript
public class Node {
public int[] address;
public int distanceTraveled;
public int accumulatedCost;
public Node prev;
public Node(int[] address, int distanceTraveled, int heuristic, Node prev) {
this.address = address;
this.distanceTraveled = distanceTraveled;
this.accumulatedCost = distanceTraveled + heuristic;
this.prev = prev;
}
}
public int heuristic(int[] current, int[] dest) {
int dx = Math.abs(current[0] - dest[0]);
int dy = Math.abs(current[1] - dest[1]);
return dx + dy;
}
public void AStar(int[] start, int[] dest) {
// Initialize our min-heap with comparator and visited set
Set visited = new HashSet<>();
PriorityQueue minheap = new PriorityQueue<>((address1, address2) -> address1.accumulatedCost - address2.accumulatedCost);
// Allowable directions for our addresses
int[][] directions = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };
// Create a starting node for our starting address
Node startAddress = new Node(start, 0, heuristic(start, dest), null);
// Add the starting address to the visited and min-heap
minheap.offer(startAddress);
visited.add(Arrays.toString(startAddress.address));
// While the min heap is not empty
while (!minheap.isEmpty()) {
// Pull the smallest item from the heap
Node current = minheap.poll();
// If we reached the destination, write out the path
if (Arrays.equals(current.address, dest)) {
while (current.prev != null) {
System.out.println('(' + current.address[0] + ", " + current.address[1] + ')');
current = current.prev;
}
}
// Loop over all directions: x + 1, x - 1, y + 1, y - 1
for (int[] direction : directions) {
int curX = current.address[0];
int curY = current.address[1];
// Add the direction to the current address
int nextX = curX + direction[0];
int nextY = curY + direction[1];
// Create a new node (neighbor)
Node neighbour = new Node(
new int[] { nextX, nextY },
current.distanceTraveled + 1, // distance traveled so far
heuristic(new int[] { nextX, nextY }, dest), // heuristic to destination
current
);
// Check if we've already visited the address
if (visited.contains(Arrays.toString(neighbour.address))) {
continue;
}
// Add the neighboring address to the visited set and minheap
visited.add(Arrays.toString(neighbour.address));
minheap.offer(neighbour);
}
}
}
import heapq
class PriorityQueue:
def __init__(self):
self.queue = []
def offer(self, item):
heapq.heappush(self.queue, item)
def poll(self):
if not self.queue:
return None
return heapq.heappop(self.queue)
def isEmpty(self):
return len(self.queue) == 0
class Node:
def __init__(self, address, distance_traveled, heuristic, prev):
self.address = address
self.distance_traveled = distance_traveled
self.accumulated_cost = heuristic + distance_traveled
self.previous = prev
def __eq__(self, other):
return self.address == other.address
def __lt__(self, other):
return self.accumulated_cost < other.accumulated_cost
def heuristic(current, dest):
dx = abs(current[0] - dest[0])
dy = abs(current[1] - dest[1])
return dx + dy
def A_star(start, dest):
# Initialize our min-heap with comparator and visited set
visited = set()
minheap = PriorityQueue()
# Allowable directions for our addresses
directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]
# Create a starting node for our starting address
start_node = Node(start, 0, heuristic(start, dest), None)
# Add the starting address to the visited and min-heap
minheap.offer(start_node)
visited.add(str(start_node.address))
# While the min heap is not empty
while not minheap.isEmpty():
# Pull the smallest item from the heap
current = minheap.poll()
# If we reached the destination, write out the path
if current.address == dest:
while (current.previous) {
printf(f"{current.address}");
current = current.previous;
}
return;
# Loop over all directions: x + 1, x - 1, y + 1, y - 1
for direction in directions:
cur_x, cur_y = current.address
# Add the direction to the current address
next_x, next_y = cur_x + direction[0], cur_y + direction[1]
# Create a new node (neighbour)
neighbour = Node(
(next_x, next_y),
current.distance_traveled + 1, # Distance from start to this point
heuristic((next_x, next_y), dest), # Heuristic cost to destination
current
)
# Check if we've already visited the address
if str(neighbour.address) in visited:
continue
# Add the neighboring address to the visited set and minheap
visited.add(str(neighbour.address))
minheap.offer(neighbour)
import PriorityQueue from "./PriorityQueue.js";
class Node {
constructor(address, distanceTraveled, heuristic, previous) {
this.address = address;
this.distanceTraveled = distanceTraveled;
this.accumulatedCost = heuristic + distanceTraveled;
this.previous = previous;
}
}
const heuristic = function (current, dest) {
const [currentSt, currentAve] = current;
const [destSt, destAve] = dest;
return Math.abs(currentSt - destSt) + Math.abs(currentAve - destAve);
};
const AStar = function (start, dest) {
// Initialize our min-heap with comparator and visited set
const visited = new Set();
const minheap = new PriorityQueue(
(address1, address2) => address1.accumulatedCost < address2.accumulatedCost);
// Allowable directions for our addresses
const directions = [
[1, 0],
[-1, 0],
[0, 1],
[0, -1],
];
// Create a starting node for our starting address
const startAddress = new Node(start, 0, heuristic(start, dest), null);
// Add the starting address to the visited and min-heap
minheap.offer(startAddress);
visited.add(JSON.stringify(startAddress.address));
// While the min heap is not empty
while (!minheap.isEmpty()) {
// Pull the smallest item from the heap
let current = minheap.poll();
// If we reached the destination, write out the path
if (JSON.stringify(current.address) === JSON.stringify(dest)) {
// Trace back the path from destination to start
while (current.previous !== null) {
console.log(current.address);
current = current.previous;
}
}
// Loop over all directions: x + 1, x - 1, y + 1, y - 1
for (const direction of directions) {
const [curX, curY] = current.address;
// Add the direction to the current address
const [nextX, nextY] = [curX + direction[0], curY + direction[1]];
// Create a new node (neighbor)
const neighbour = new Node(
[nextX, nextY],
current.distanceTraveled + 1,
heuristic([nextX, nextY], dest),
current
);
// Check if we've already visited the address
if (visited.has(JSON.stringify(neighbour.address))) {
continue;
}
// Add the neighboring address to the visited set and minheap
visited.add(JSON.stringify(neighbour.address));
minheap.offer(neighbour);
}
}
};
*Note: Python doesn't have a min-heap / priority queue data structure so you can use heapq, similarly JavaScript doesn't have one however you can grab mine from here or import another.
I know that was a lot of reading and a lot of code, but I hope that it all came together towards the end. I also hope it's a little easier now to see the potential applications of A*. It's widely used in video games for NPC's, AI systems such as machine learning, networks, robotics as well as surprise surprise, route planning.